x2-11x+28=0: Quadratic Expression

Read Time:4 Minute, 15 Second

x2-11x+28=0 is a mathematical equation, that comes under a specific quadrant of its world. It is calculative questions where variables and numbers are given to evaluate the value of ‘x’. The given equation is one of the form of a quadratic equation. It is a part of maths which requires a formula to solve it. This equation will test your mathematical knowledge and abilities. Such forms of mathematics improve ours thinking ability. This quadratic equations problem is easily solve by applying quadratic formula.

About Quadratic Equation

It is a problem-based equation that is asked to be solve to prove a solution. It is derived from a Latin word quadratus.

In this equation x2-11x+28=0, we have to prove that left hand side is equal to right hand side (L.H.S = R.H.S) by finding the value of x. Mathematical equations are just seemed to be complex but they’re actually difficult.

Quadratic equation is a mathematical term. The given equation is a prime example of quadratic equation. Quadratic equations are represented in the form of ax^2 + bx + c = 0.

Example: In the given equation, ax^2 + bx + c = 0

The term a, b, c are known as coefficient, a is not equal 0. The term ‘x’ is represented as variable.

Q. Let Find the Solution of the x2-11x+28=0

The given equation is a quadratic expression. It requires a specific formulas to solve such the world of mathematical expressions.

Solution:-

We will solve the equation by quadratic formula, which is given below

In this given equation: a = 1, b = -11 and c = 28 where a is not equal to 0. The term ‘x’ is an unknown factor.

To solve the given problem we need to place the values on the quadratic formula by Al-Khwarizmi.

Assume, X = x

We get two types of equation one is positive and other is negative such as

Thus, we got the solution where, x = 7 and x = 4

Now, by applying any value of x from the two in the equation we can prove that the equation is correct.

Let’s apply value x = 7, in the equation.

x² – 11x + 28 = 0
As, x= 7

The equation will be;

= (7)² – 11 ( 7 ) + 28 = 0
= 49 – 77 + 28 = 0
= – 28 + 28 = 0
= 0 = 0 => Hence, (L.H.S = R.H.S)

Hence, it is proved that the equation is an example of quadratic equation.

Further calculation, for explanation purpose.

Even if we apply the value x = 4, will be getting the same results.

Let’s apply x = 4, in the equation
x2 – 11x + 28 = 0

The equation will be;

= 16 – 44 + 28 = 0
= – 28 + 28 = 0
= 0 = 0 , which is also gives L.H.S = R.H.S.

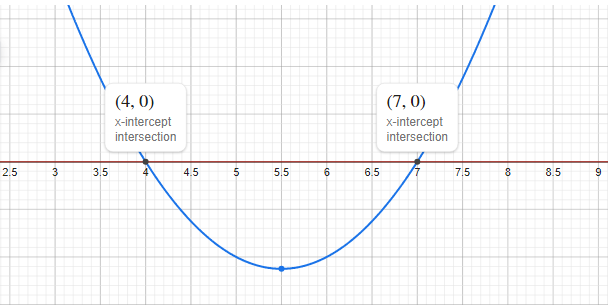
Graph of x2-11x+28=0

The given co-ordinates of the given eqaution x2-11x+28=0 are X = (4 ,0) and X = (7 ,0).

Explain the Steps above to Solve the Equation x2-11x+28=0?

Using Quadratic Formula: The quadratic formula is used to ease the calcuation, by simply adding all the respective values in this formula we can find a right solution.
Simplification: Simplification is a method to solve an equation by splitting the middle terms of the equation. This technique is used to determine the factors of an equation to solve.
Taking the Square Root: In this technique we have separated the square terms and the constant term opposite to each other. Square root out is a method to find a solution for solving Quadratic Equation. In this technique we solve the roots of both the sides to get an accurate answer for this.
Completing the square: Divide the equation by the coefficient of square variable. It means divide the equation by the coefficient ‘a’ then imply the square method. Add a constant term on both the sides of the equation to find the value.

Two Forms of Quadratic Equation

Standard Form: This form is represented by y = ax² + bx + c, where a, b, c are numbers and x is a variable.
Factored Form: This form is represented by y = ( ax + c ) ( bx + d), where a, b, c, and d are just numbers.

Can we consider coefficient ‘a’ as zero in a quadratic equation?

If the coefficient ‘a’ is represented with value 0 then it will change the whole form of equation. It will get converted to a linear equation from the quadratic equation.

Conclusion

x2-11x+28=0 equation can be solve by four different methods. The equation can be asked in the format of multiple choice questions also. By breaking down the value of ‘x’ we have found the right solution for the term.

To find the solution for the above listed three equations, same quadratic formula is used to find the value of ‘x’. Quadratic equations is a small universe in the cosmos of mathematics, it may includes complex situation but it is used for simplification only

Also, Read About:-

x*x*x Is Equal To 2: Lets Find The Solution